By Jonas Nick

Introduction

This article is about the recent introduction of so-called x-only pubkeys to the Bitcoin Improvement Proposal BIP-schnorr. The BIP defines the introduction of Schnorr signatures for Bitcoin.

Schnorr signatures have the potential to provide a variety of benefits over the existing signature scheme on Bitcoin (ECDSA), in particular smaller transaction size (and weight) for typical transactions. This is achieved partly because Schnorr signatures support the aggregation of multiple signatures into a single signature more easily.

With x-only pubkeys we can squeeze out even more optimization, significantly reducing the weight of every transaction output without any loss in security.

Background

By removing the Y-coordinate byte from compressed public keys currently used in Bitcoin, public keys end up with a 32-byte representation. We are going to look at how it works, why that’s useful, and sketch a security proof.

Sketching a security proof is a technique that can be useful in Bitcoin and Lightning protocol research in general. It will demonstrate that dropping the byte does not weaken the security — not even by a “single bit”.

To keep this a nice and small post we will not do this formally precise. The main goal of this article is to provide a basic understanding for the x-only part of BIP-schnorr.

This article assumes that the BIP-taproot softfork is activated, which defines SegWit version 1 output spending rules. We don’t care what the new output spending rules are except that one of the new rules is that spending is allowed with Schnorr signatures as defined in BIP-schnorr. It is important to point out that the BIPs are only proposals, so there’s no guarantee that a BIP-taproot activates in its current form or at all.

Let’s first look at how compressed public keys work today in Bitcoin.

A compressed public key in Bitcoin is either the byte 2 followed by a 32 byte array or the byte 3 followed by a 32 byte array. The first byte is called the tie breaker and the second part is the X-coordinate of the underlying point on the elliptic curve.

What is the purpose of the tie breaker?

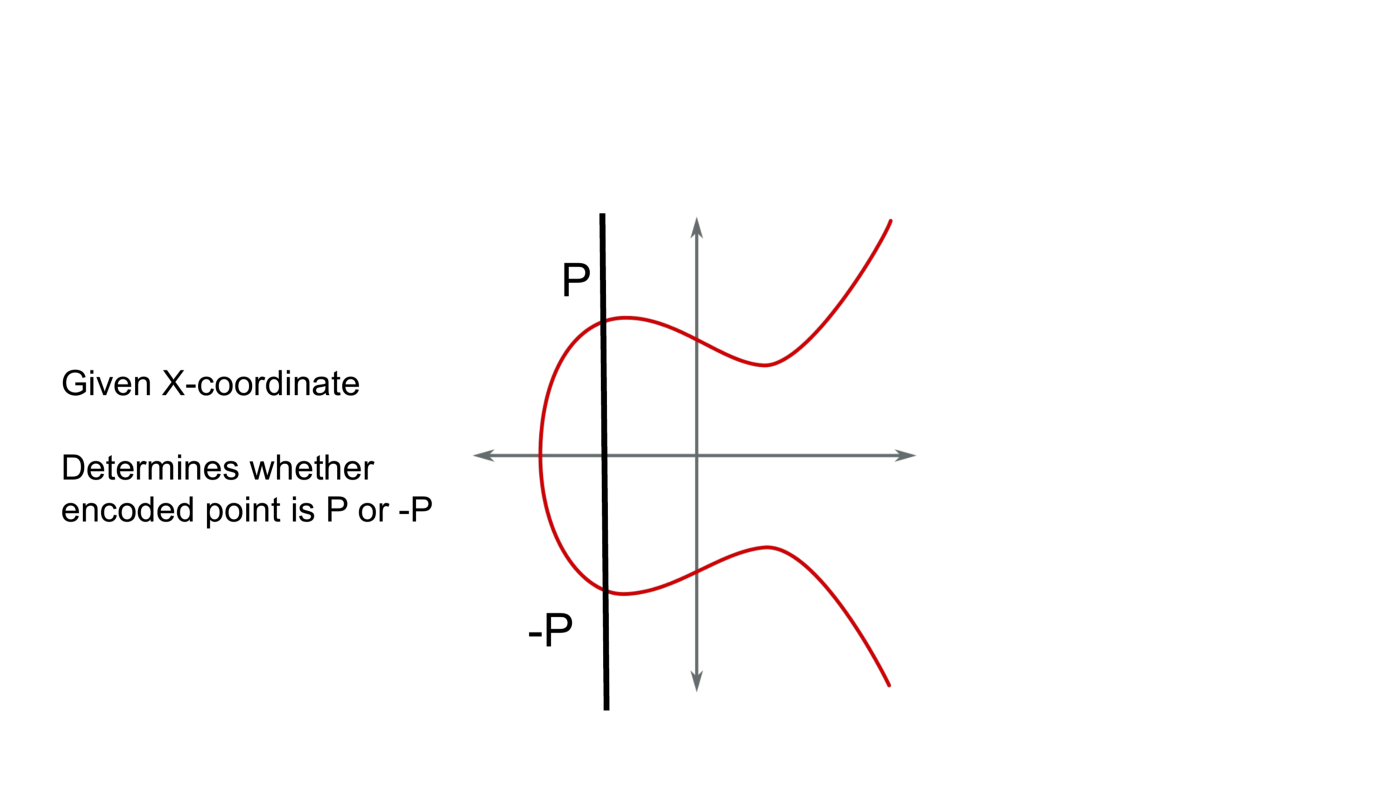
A public key encodes a point on an elliptic curve. Given only an X-coordinate there exist two points on the curve. The purpose of the tie breaker is to determine which one of the two points is encoded, P or -P.

Recently BIP-Schnorr was changed from using compressed public keys to use x-only public keys. The difference is that the tie breaker is not part of the public key anymore. Instead it is implicitly assumed that the tie breaker is 2. Actually, a different tie breaker is used in the BIP but that doesn’t matter for the purpose of this article.

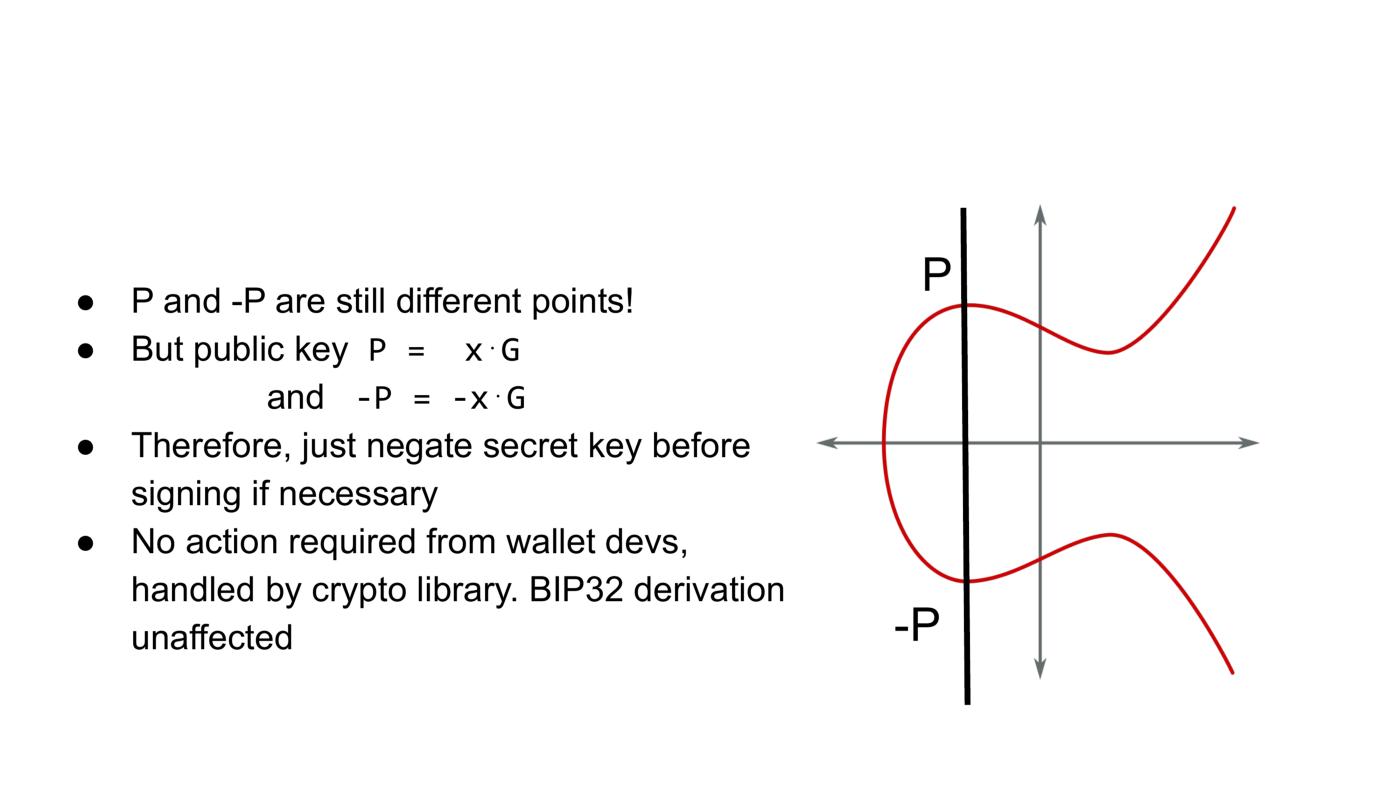
So why does this work? P and -P are still different points after all. The public key point P generated by secret key x is x times the generator of the group G. The secret key for public key -P is -x. The answer is that we just need to negate public and secret keys at the right time. In particular, the signing algorithm will check that you’re signing for the correct public key, and negate the secret key if necessary.

It is important to note that there’s no action required from wallet developers. It should be handled by the underlying crypto library. And also BIP32 hierarchical deterministic wallet generation works just as before, except that you throw away the first byte.

Why introduce x-only pubkeys?

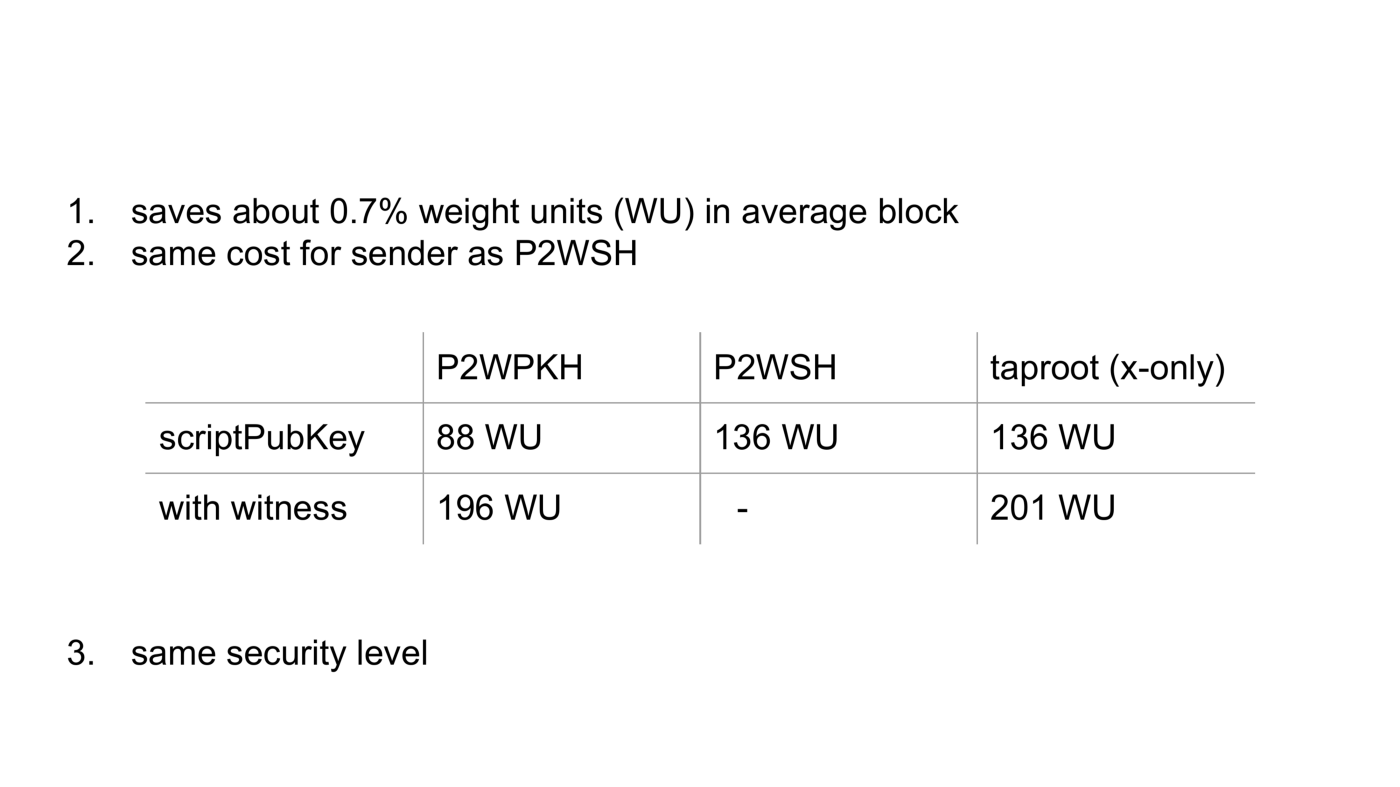
First of all, scriptPubKey bytes are expensive in terms of weight units: x-only saves about 0.7% weight units in average full blocks. Second, the cost for the sender creating a scriptPubKey is the same as in pay-to-witness-script-hash, 136 weight units. In theory, adoption of Taproot would be slower if it was more expensive than the older segwit version.

Pay-to-witness-pub-key-hash scriptPubKeys still have far less weight than Taproot outputs, because they only include the 20-byte hashed public key, but that would be insecure for Taproot.

Just to complete the picture, if we take the witness weight into account, Taproot and pay to witness pubkey hash are very similar.

Proof sketch

Now let’s look at why this is secure.

What we know is that in the random oracle model if the discrete logarithm problem is hard, then Schnorr signatures are secure.
This means that no signatures can be forged without knowledge of the secret key.

Now what we want to prove is if Schnorr signatures with compressed public keys are secure, then x-only Schnorr signatures are secure. Or equivalently, if x-only Schnorr signature are insecure, then Schnorr signatures are insecure.

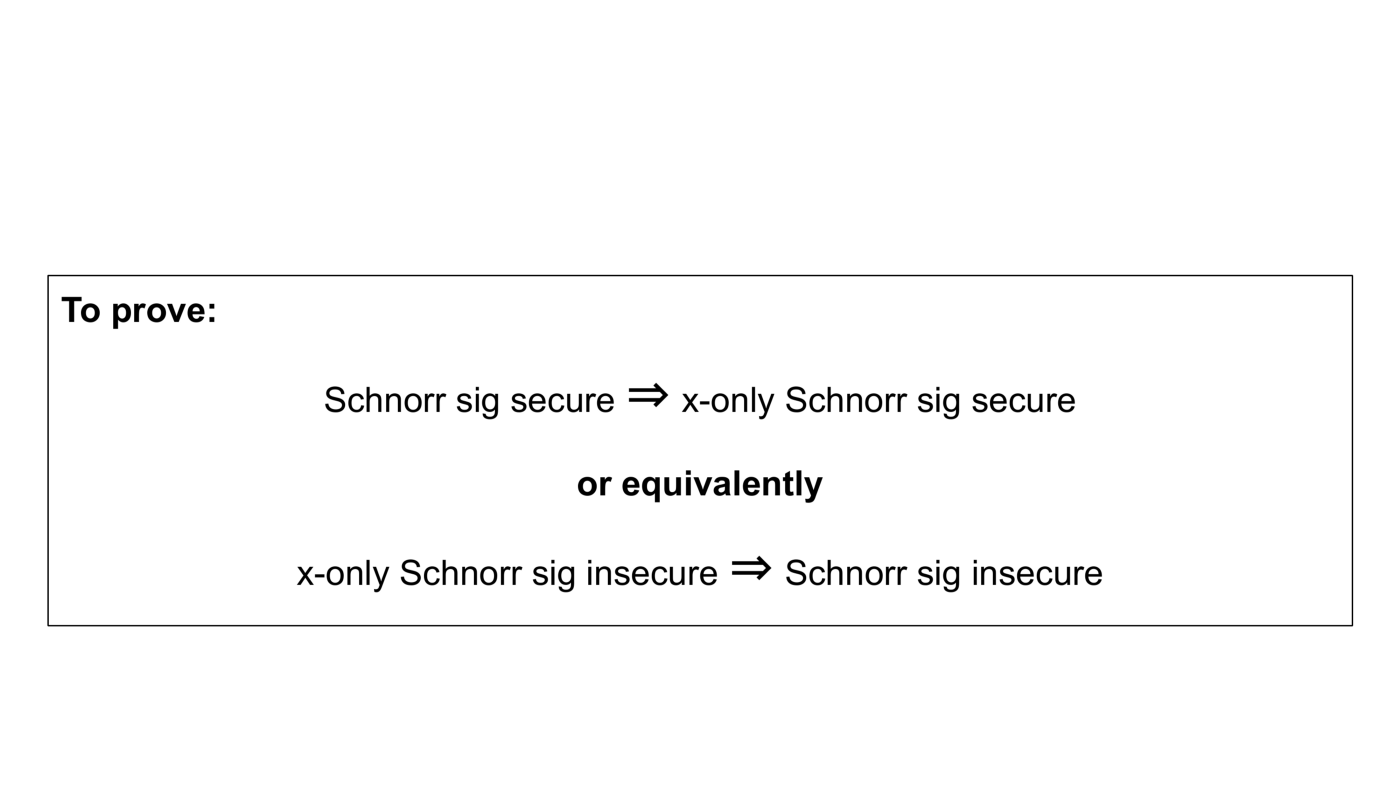
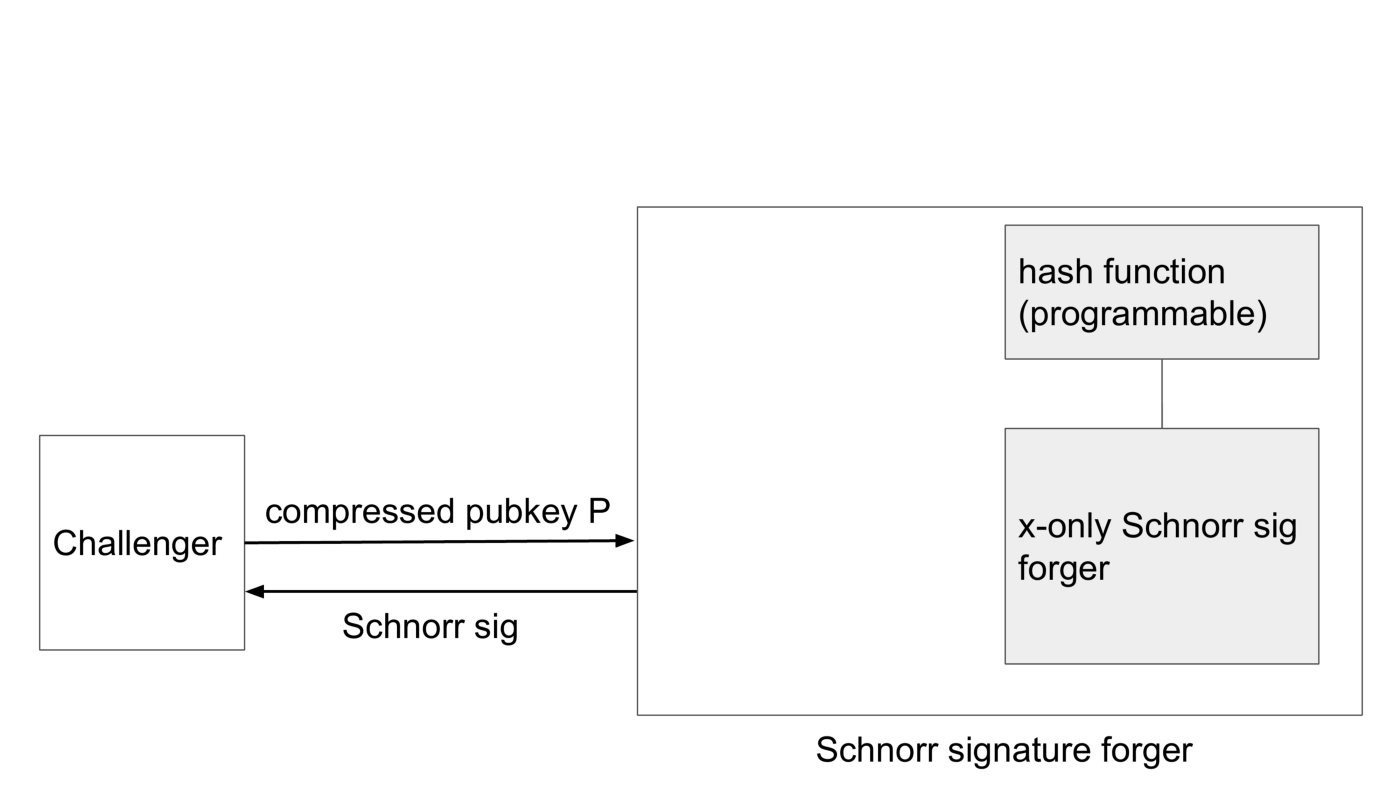
So we assume that an algorithm exists that forges Schnorr signatures as depicted on the right in the diagram below.

Schnorr signatures are a tuple. The first element is the public nonce and is generated by multiplying the secret nonce with the group generator.
The second element combines the secret nonce and the secret key x. The only part that’s important here is that the Schnorr signature involves some hash computation. What we’re assuming now, is that at some point the forger must compute the hash — there’s no other way to produce the forgery. In order to define this correctly in formal proofs the hash function is replaced with an idealized device called Random Oracle. For the purpose of illustration we will continue to call this hash function.

Now what we have to do is build an algorithm that responds to a challenger providing a compressed public key and expects a Schnorr signature forgery in return. We will somehow make use of the x-only Schnorr signature forger. It’s just an algorithm and we can run it on our virtual machine if you will. Moreover, we can patch the forger’s code that computes the hash function to do return anything that we want. The replaced hash function must be randomly looking to the x-only Schnorr signature forger because otherwise it can detect that it is in a simulation and behave differently.

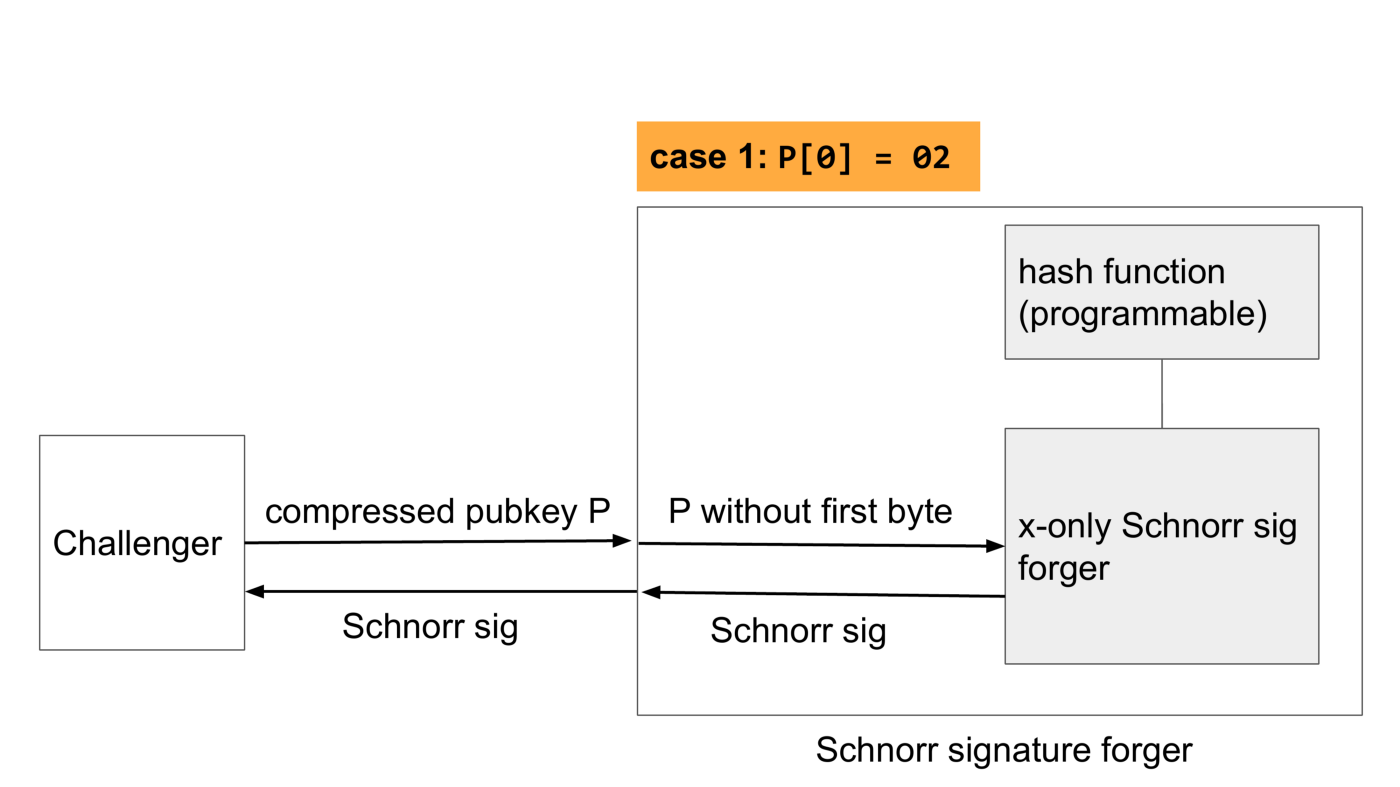
Now let’s look at the first case where the first byte of the public key is 2, the same as what we’re implicitly assuming with x-only pubkeys. In that case we just need to remove the first byte, pass it to the forger, let it do its thing and pass the Schnorr signature to the challenger.

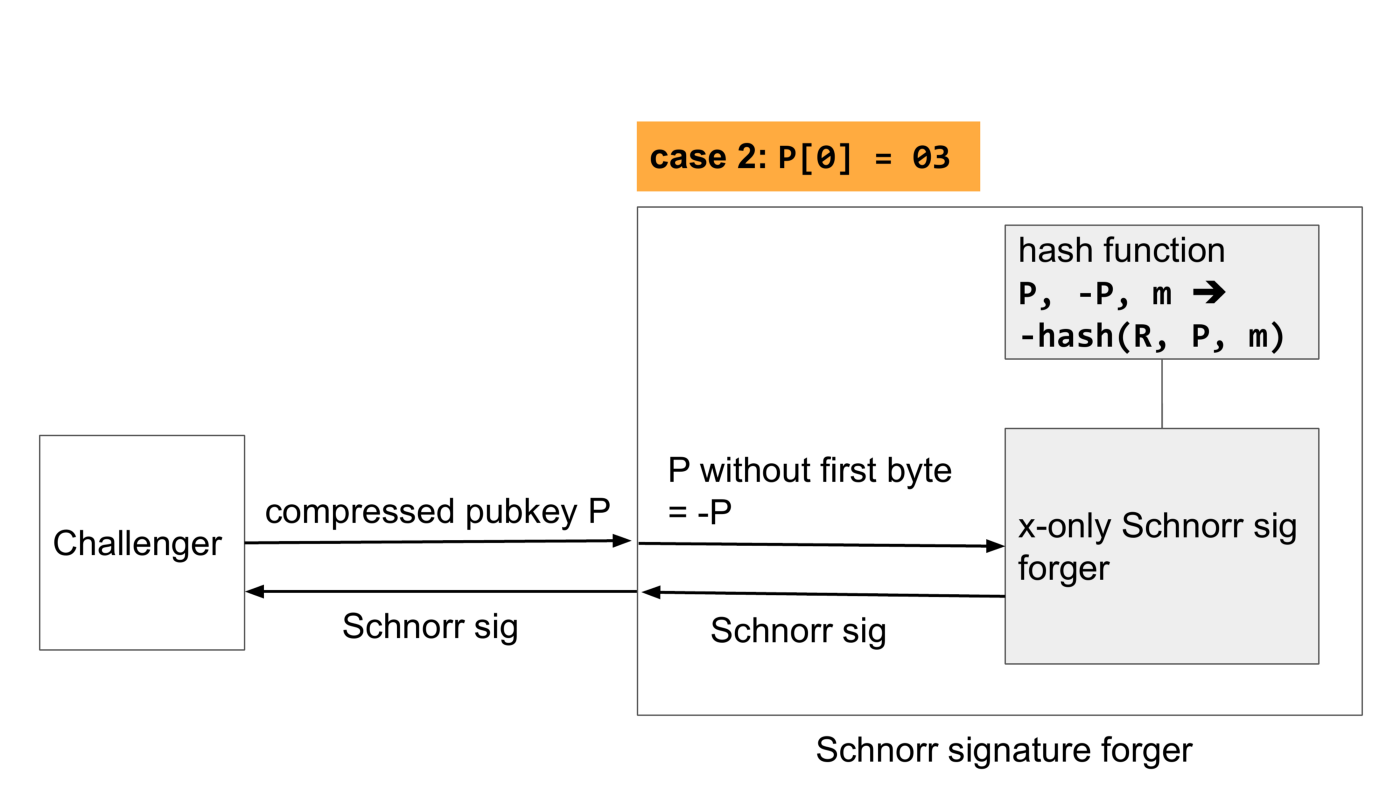
In the other case the first byte is 3. Again, we pass the pubkey without the first byte to the forger, but now the x-only forger will decode the public key as -P, so the signature that will be created will be for the wrong public key. We fix this by programming the hash function to return the negative of the output of the hash function that the challenger uses. Then we just wait for a reply from the forger and pass it to the challenger.

The negated hash results in a Schnorr signature for the negated point, so the challenger will happily accept the signature.

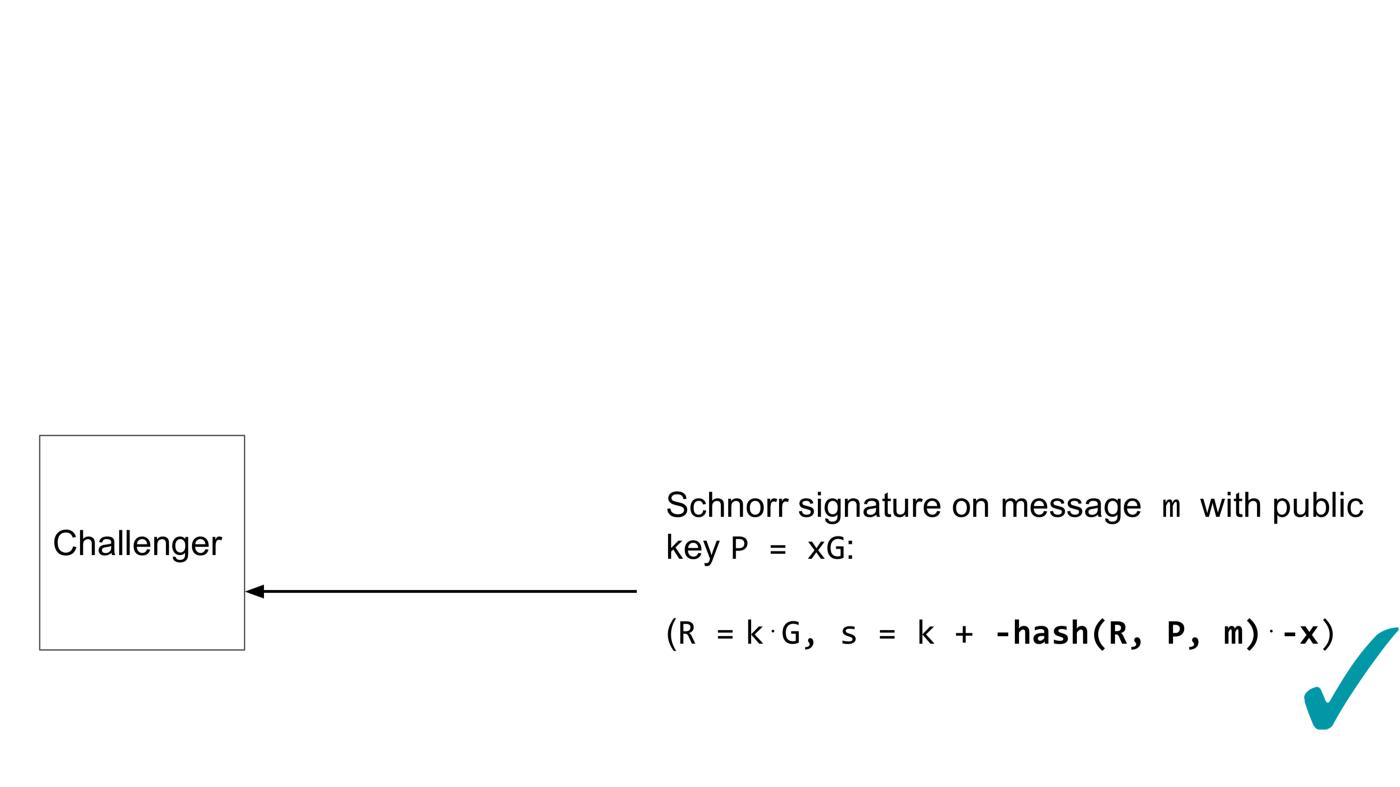
To summarize, what we’ve shown is that if an x-only Schnorr signature forger exists, then a compressed pubkey Schnorr signature forger exists or equivalently we can assume x-only Schnorr signatures are secure.

We’ve also shown the somewhat unintuitive fact that the hardness of breaking x-only is equal to breaking the compressed pubkey signature scheme. In short, the tie breaker never added anything to the security of the scheme in the first place; an attacker can simply negate the key if necessary before applying the x-only attack. Compared to the group operation (in this case point addition) whose number is often counted when giving bounds on the hardness of an attack, the negation operation is trivial. In secp256k1’s case, it’s just the negation of an integer (the Y coordinate) modulo the field order, which is close to 2²⁵⁶. That takes almost no time on any modern processor (a few nano seconds on my laptop) and means that concretely the difference in hardness is negligible.

Conclusion

In conclusion, BIP-schnorr and BIP-taproot were adjusted recently (September 2019) to use 32 byte x-only public keys. This will further optimise the already low transaction weights if and when Schnorr signatures are adopted on Bitcoin.

This change is relatively low level, and wallet developers don’t have to care much about it. The security of x-only Schnorr signatures can be reduced to Schnorr signatures with compressed keys.

BIP-schnorr and BIP-taproot are slowly maturing from the draft status to the proposal status. We’re looking for feedback, so feel free to read the BIPs, implement them, or play with implementations of BIP-schnorr and BIP-taproot. Very good resources for learning more about the BIPs are this Jupyter notebook from the Optech Taproot workshop and the Taproot Review Club.

Note: This blog was originally posted at https://medium.com/p/f86476af05d7