Introduction

This is the first in a series of posts about about covenants in Bitcoin using Taproot and a (hypothetical) CAT opcode. Historically, and as has been implemented in Elements, CAT has been considered to be a covenant opcode only in conjunction with CHECKSIGFROMSTACK. In this post, which will be much mathier than later ones, we'll talk about how to abuse the math of Schnorr signatures to emulate the functionality of CHECKSIGFROMSTACK.

First, some preliminaries. A covenant is a hypothetical Bitcoin Script which restricts the form of the transaction spending the coins. Ordinarily, Script can only require the presence of certain authentication data for spending: signatures, hashlock checks, etc. Script cannot enforce velocity limits, restrict coins to going to certain locations, or anything like that, because the Script execution environment does not have access to transaction data. Ultimately, adding covenants to Bitcoin would mean adding the ability to introspect transactions to Script.

Secondly, CAT is the "concatenation" opcode. Originally present in Bitcoin but quietly removed in 2010, CAT takes two elements from the stack, concatenates them, and pushes the result onto the stack. It can be used to assemble large stack items from small ones, or to split large items into smaller ones. CHECKSIGFROMSTACK, which has never been in Bitcoin, is an opcode which allows the user to check signatures on arbitrary data, unlike the CHECKSIG opcode which checks a signature on the spending transaaction.

The combination of CAT and CHECKSIGFROMSTACK gives you transaction introspection in a somewhat clever way: the user provides data for the entire transaction on the stack; using CAT, the script bundles this all up into one item, which it hashes and passes to CHECKSIGFROMSTACK to validate a signature on the data. It then passes the same signature, with the same key, to CHECKSIG. If both checks pass, the user-provided transaction data must have been the actual transaction data. It is then straightforward to use Script to do whatever checks on this data your covenant requires.

ECDSA and Almost-Covenants

Suppose we had CHECKSIGFROMSTACK but not CAT. Then in principle, we could do a very simple sort of covenant: one where the user provides the hash of all the transaction data and the script checks a signature on this using both CHECKSIG and CHECKSIGFROMSTACK. Without CAT, the script can't recompute the hash from individually-checkable data, so all it can really do is check the hash for equality against a specific value, meaning the coins are restricted such that they can only be spent by a single specific transaction.

It is straightforward to generalize this to a choice of a small number of transactions, but open-ended predicates like “any transaction whose outputs are less than 1 BTC” are out of the question.

It turns out this sort of covenant can’t work, for a technical reason: the transaction data that CHECKSIG checks always includes the txid of the previous transaction, which is a hash of (among other things) the covenant script itself. (This isn't quite true because of the SIGHASH_SINGLE bug but for our purposes this doesn't help anything.) So to be effective, the script would need to include its own hash, which is impossible.

What makes this observation interesting is that Bitcoin today actually has a way to get the transaction hash onto the stack like this, which means that if it weren’t for this hash circularity problem, Bitcoin would have Covenants today. And if there were a way to sign transaction data that didn’t include data from the previous transaction, for example, using the SIGHASH_NOINPUT proposal which is so popular in the Lightning Network world, Bitcoin would have covenants. Let's see how this works:

ECDSA signatures work as follows: you have a keypair (x,P=xG) which are your signing and verification keys, respectively. If you’re not familiar with the mapping x↦xG, it maps scalars (integers modulo some large prime) to elliptic curve points (pairs of integers modulo some different prime, which satisfy some particular equaton). What’s important is (a) it’s homomorphic, so (x+y)G=xG+yG, and (b) it’s believed to be impossible to reverse without a quantum computer. Aside from these two facts it’s not important what this mapping looks like on an algorithmic level; we’ll just treat it as a black box.

To produce an ECDSA signature, you generate an ephemeral keypair (k,R=kG) then compute the value r which is the first component of the point R, coerced from an integer modulo the non-scalar prime to an integer modulo the scalar prime. (This design decision was made for legal reasons, by the way — incomprehensibility counts as novelty, for patent purposes, so this design did not violate any existing patents.) You then compute the value

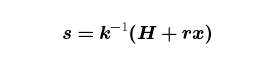
where H is the hash of your transaction data. Let’s rearrange this by multiplying both sides by k then running everything through the ⋅↦⋅G⋅ map:

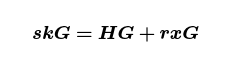
which, for greater clarity, is

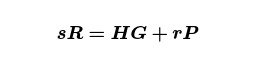
Rearranging one more time, we get

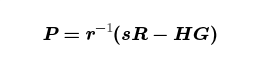
which, for fixed R and s, is a cryptographic hash of the transaction data as long as H is. As it happens, Bitcoin Script has an opcode for “for fixed R and s, compute H and give me such a P”: CHECKSIG.

Concretely, consider the script DUP <fixed signature> SWAP CHECKSIGVERIFY. This can only be satisfied if the user puts a satisfying pubkey P on the stack. The script duplicates it, swaps it with a fixed signature, then calls CHECKSIGVERIFY on <sig> <P>. If the above equation is satisfied, these are consumed, leaving the copy of P on the stack. If not, the script fails and the transaction is invalid.

There are two lessons to take from this: first, that it is really easy to get covenants in Bitcoin; second, by abusing the algebra of digital signatures, it’s possible to get transaction data onto the stack using signature-checking opcodes.

BIP340 Signatures and Key-Prefixing

Taproot includes a variant of Schnorr signature called a BIP340 signature. These signatures use the same keys, same elliptic curve, and same group of scalars, but the signing algorithm is much simpler: you compute the ephemeral (k,R=kG) just like before, but this time

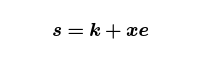
where e is a hash of your public key P, the ephemeral key R, and the transaction data. Recall that the reason we couldn’t get covenants from ECDSA was that our script would wind up going into the transaction data, so any target values for P would wind up in our message hash, but since P itself was supposed to be the hash, we had a circularity and we were stuck.

It would appear that BIP340 puts the nail in the coffin of this style of covenant: P shows up explicitly in the signature hash, so no matter what crazy future sighashing schemes might get included in Bitcoin, this circularity will remain and we are stuck. In fact, this inclusion of P means that BIP340 signatures aren’t just signatures, but “signatures of knowledge”. This is a term of art which means, roughly, that you are not able to run these signatures backward in any sense. For a long time, I thought this meant that I couldn’t abuse BIP340 signatures to get non-signature behavior out of them.

In fact, I was wrong, although I need CAT to get really interesting behavior. The trick is that, while I can't fix s and R to get a transaction hash out of P, I can fix R and P to get a transaction hash out of s. And in fact, the resulting transaction hash is a "real" hash, in the sense that there aren't any un-Script-able elliptic curve ops involved in it.

Let’s be specific: consider the script 2DUP CAT ROT DUP <G> EQUALVERIFY CHECKSIG. This

• takes as input a signature in two pieces, so our stack is R s;
• 2DUP CAT duplicates both pieces and concatenates the copy, leaving the stack as R s Rs
• ROT DUP moves the R to the top of the stack and duplicates, leaving s Rs R R
• <G> EQUALVERIFY consumes the top R and forces all of them to be the EC group generator G
• CHECKSIG interprets the remaining R as a public key, which it verifies the signature Rs with, consuming both
• Now only s is on the stack.

Yikes. What is going on here? Well, the step where we force both R and P to be the group generator is equivalent to forcing our secret keys x and k to be 1. Our BIP340 signature equation is then

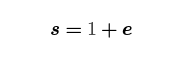
i.e. the s that our script leaves on the stack is actually a SHA256 hash of our transaction data, prefixed by a couple copies of G (and a couple copies of SHA256("BIP0340") because BIP340 loves itself). Veeery interesting. Script has an opcode SHA256, and we have CAT in the hypothetical world of this post, so if we could somehow deal with this +1, we'd be able to have the user provide transaction data which we could constrain then validate against this hash, just like if we had CHECKSIGFROMSTACK.

In fact this +1 is super easy to deal with. We just require the user grind her transaction data until the actual hash ends in the byte 01, which is pretty cheap (takes 256 tries on average, which at 250ns per shot would take 64 microseconds, comparable to the signing algorithm itself). Then her s value will end it 2, which we enforce by asking her to leave it off; we'll add it ourselves. Concretely we add a 2 CAT after the 2DUP in our script, where we're computing s for the signature check, and 1 CAT to the end of our script where we want the result to be our transaction hash. Voilà.

Next Steps

This has been a trip: it turns out that the BIP340 signatures in Taproot, while designed to be more “covenant-proof” than the old-school ECDSA signatures, actually leave us much closer to covenants. Indeed, all we need is CAT to get CAT+CHECKSIGFROMSTACK-style covenants.

However, there is a problem if we hope to do construct recursive covenants, which dynamically restrict transaction output scripts to follow certain templates. In Taproot, transaction outputs are EC public keys, which commit to scripts using an elliptic-curvy hash we don’t have in Script. …Or do we?

I believe the answer is no, but I also believe that we can do some very interesting things with this nonetheless.

A natural question to ask is, are these sighash-templating covenants powerful enough to actually do anything, given the consensus limits of Script? Readers may recall that we blogged at Blockstream four years ago about this but never followed up with practical applications. My belief now is that the dearth of applications was more a consequence of the incredible difficulty of reasoning about and constructing Script, and that Miniscript has since provided some new ways of thinking that will accellerate this kind of development. And indeed, if you really want to dig into Script, you can construct some pretty cool things with CHECKSIGFROMSTACK.

In our next posts, we’ll talk about how to use auxiliary inputs to simulate SIGHASH_NOINPUT and enable constant-sized backups for Lightning channels, and how to use "value-switching" to construct Vaults.

In our final post we’ll talk about ad-hoc extensions of Miniscript, and how to develop software for these constructions in a maintainable way.

Note: This blog was originally posted at https://medium.com/blockstream/cat-and-schnorr-tricks-i-faf1b59bd298